皆さんは「囚人と帽子のパズル」というパズルをご存じでしょうか?
このパズル自体は、古くから存在するパズル問題で、最近では論理的思考力を試す試験などで出題されることもあるようです。
このパズルの面白さに魅了され、私は現在このパズルをテーマに、数学専攻の博士課程大学院生として研究を行っております。
今回はそんな私が、この「囚人と帽子のパズル」の魅力をたっぷりお伝えしたいと思います!
囚人と帽子のパズル(初級編)
囚人と帽子のパズルは様々なバリエーションがありますが、まずは一番簡単なバージョンを紹介します(この記事では単に帽子パズルと呼んでいくことにします。)
パズル1 (簡単バージョン)
看守がとあるゲームをするために2人の囚人を同じ部屋に入れ、帽子を1人に1つずつ被せます。

ルール
- 帽子は黒か白のどちらかの色で塗られている。
- 囚人は自分の帽子の色はわからないが、もう1 人の帽子の色は見えている。
- 2人の内、1人でも自分の帽子の色を正解すれば、囚人側の勝利で釈放、2 人とも不正解ならば囚人側の敗北で処刑される。
- 囚人が部屋に入ってからはコミュニケーションを図ることはできない。
- 看守がどのように帽子を被せるかは囚人は入室するまで知らない。
- このゲームのルールや勝利条件については、部屋に入る前の囚人に伝えられ、ゲーム開始までに2人で戦略を相談することができる。
はたしてこの時、どのように帽子を被せられても、常に囚人側が勝利する戦略は存在するでしょうか?
↓(自分で考えたい方は、答えを見る前に、ちょっと考えてみてください)
↓
↓
↓
↓
↓
↓
↓
答え:「常に囚人側が勝利する戦略は存在する」
そして、その戦略とは、
1 人の囚人は見えた相手の帽子の色と同じ色を発言し、もう 1 人は見えた色とは違う方の色を発言する。
というものです。
なので、ゲーム開始前に2 人はどちらがどの役割を担うか相談しておけばよいことになります。
・・・看守がどのように帽子を被せるか分からないのに、本当にそんな戦略で常に 1 人は正解できるのか??と疑問の思う方もいるかもしれないので、少し記号なども用いて整理して解説してみます。
まず、2 人の囚人を a, b とおくことにします。

そして 2 人は相談によって
- a は見えた色(bの帽子の色)と同じ色
- b は見えた色(aの帽子の色)と異なる色
を発言することになったとします。
このとき2 人の囚人に黒白の 2 色の帽子を被せる組み合わせは計 4 パターンになります。

4 つの帽子の被せ方にそれぞれ f1, f2, f3, f4 と名前を付けておきました。つまり f1 は看守が 2 人ともに黒と被せた場合にあたります。
例えば f1 においては囚人 a は、自分が見えた相手の帽子の色、つまり囚人 b が被っている帽子の色と同じ色を発言したいので、「黒」と発言します。
そして囚人 b は、自分が見えた相手の帽子の色と違う色、つまり囚人 a が被っている帽子の色と違う方の色を発言したいので、「白」と発言します。

すると囚人 a は被っている帽子の色と発言した色が一致しているので正解となり、残念ながら囚人 b は不正解でしたが、勝利条件「1 人以上正解である」はみたしているので、囚人側の勝利となり、2 人とも無事釈放されます。
これは f1 だから勝利できたわけではありません。その他の 3 つの状況においても、必ず 1 人は正解することができています。
各帽子の被せ方と、各囚人がどのような色を発言したかをまとめた表は以下のようになります。正解した囚人の行には色が付いています。
表のそれぞれの場合を見てもらえれば、確かに 1 人は正解していることがわかります。

これにて、パズル 1 は解けていることがわかりました。
しかし、ここで「なぜ囚人側に必勝戦略があったのか」が気になります。
はたして、今回の帽子パズルの設定を変えてしまえばどれくらい同じような結果が成り立つのか・・・?
そこから一般化された結果などが知りたくなるのが数学者というもの!
かくいう私もその 1人です。私の研究では、この囚人の「人数」や、「色の数」という設定を増やしていくだけでなく、「囚人が無限にいたらどうなるか?」、「被せられる帽子の色の候補が無限にあったらどうなるのか?」などと設定を変えたりしながら、この帽子パズルを研究しています。
そもそも、「パズルに対して数学はどう役立つのか」、「 無限というものは数学でどう扱えるのか」などを話さないことには、私の研究の面白さも伝えにくいのではないかと考えました。
なので、今回は先ほど述べたような流れで、じっくりと解説していきたいと思います。
囚人と帽子のパズル(中級編)
では、さっそくパズル 1 を拡張、つまりより難しく、解きにくくしてみましょう。
今回のパズルでは
囚人の人数を 2 人→ 5 人、色の数を 2 色→ 5 色 に増やします。
先ほどのパズル 1 では、各囚人から見た、帽子の見え方は
「自分以外の他囚人の全ての帽子が見えている」と捉えると、
今回の新たなパズルでは、
「5 人の囚人全員は自分以外の 4 人の帽子が全て見えている」ことになります。
囚人たちの勝利条件は、先ほどのゲーム同様、「1 人でも正解する」とします。
それ以外のゲームの進め方などは、全て先ほどのパズルと同じとします。
さて、これで新たなパズルが 1 つ出来ました。
このパズルを以下のようにまとめておきます。
- 囚人の人数が 5 人、帽子の色の数が 5 色であること以外はパズル 1 と同じ
- 常に囚人側が勝利する戦略は存在するでしょうか?
パズル 1 では囚人側に必勝戦略が存在しました。
はたして、人数・色の数が変わったこのパズルでも、必勝戦略は存在するでしょうか?

↓(自分で考えたい方は、答えを見る前に、ちょっと考えてみてください)
↓
↓
↓
↓
↓
↓
↓
答え:「常に囚人側が勝利する戦略は存在する」
しかし、その戦略はパズル 1 のようには簡単に説明する・言い表すことはできません。
そこで、今回は数学を使わない答え方、あえて数学を使った答え方を紹介します。
その答えを理解するために、一度パズル1にもどり、パズル1についてもう少し詳しく考えてみることにします。
ここで、もし数学を使った答え方が理解できたならば、パズル 2 にもすぐに応用できるはずです。
囚人と帽子のパズル(初級編)の解説
数学を使わない答え方
パズル 1 における帽子の被せ方のパターン 4 つ(表 1)を見ると、
- 2 人が同じ色を被っているもの(f1 と f4)
- 2 人が別々の色を被っているもの(f2 と f3)
の 2 パターンに分かれます。そして看守がどのように帽子を被せても、2 人が同じ色を被っているか、別々の色を被っているかのどちらかになります。
つまり
- 見えた色と同じ色を答えていた囚人 a は2 人は同じ色を被っていると思って発言している
- 見えた色と違う色を答えていた囚人 b は2 人は違う色を被っていると思って発言している
ということになり、必ずどちらかの思惑通りになるわけですから、常に 1 人が正解することになります。
先ほどの表 1 に、各囚人の思惑と、各帽子の被せ方が 2 人とも色が同じなのか違っているのかの情報も加えた表が以下になります。各囚人の思惑通りになっているときに、確かにその囚人が正解することが確認できると思います。

しかし「何故必勝なのか?」という問いに対して、この答え方では 5 人 5 色の場合になったときには応用できそうにありません。なので少し数学の力を借りることにしましょう。
数学を使った答え方
これまで 2 人の囚人を a, b と名付けてきましたが、ここからはあえて 囚人をa0, a1 とすることにします。この変更の意図は、その添え字によって偶数か奇数かで区別できるからです(あとでも詳しく述べます)。そしてここからは色を黒・白ではなく、数の 0, 1 に置き換えます。ここまでの名前の置き換えによって、先ほどの帽子の被せ方の表 1 は以下のように変わります。
この表にどんどん情報を追加していきます。

帽子の色が数に置き換わったことで、囚人の発言した色という情報も数に置き換わります。

そこから、各囚人ごとにその見えていた色(数)と発言した色(数)の合計という情報を先ほどの表に追加します。

上の表では、例えば、なぜ f2 の a0 部分の「合計」項目に 2 という数が入っているかというと、「a0 が見えたa1 の被っている色(数)である 1 」と、「a0 の発言した色(数)である 1 」の和が 2 だからです。
同様の理由で、他の合計の部分も計算して書き込んであります。
さらに各帽子の被せ方ごとに、その帽子の色(数)の合計という情報も最下段に追加したものが以下の表です。

これで表が完成しました!
それでは、この表を見ながら数学的に考えていきます。
まず帽子色の合計に書かれている数字を見ると、帽子色の合計は 0, 1, 2 のいずれかです。そして各帽子の被せ方における正解者を見ると、先ほど追加した「合計」項目と帽子色の合計が一致しています。
これはどういうことかというと、
まず事実として数値に置き換えた帽子色の合計は必ず偶数(2 で割り切れる数)か奇数(2 で割って 1 余る数)のいずれかになります。
そして
- 囚人 a0 は自分と相手の帽子色の合計が偶数になると思って発言している
- 逆に囚人 a1 は自分と相手の帽子色の合計が奇数になると思って発言している
ということになります。
先ほど囚人の名前をa, b から a0, a1 に変えたのは、それぞれの添え字 0, 1 が、2で割って 0 余る数・2 で割って 1 余る数、つまり偶数・奇数を表しています。
よって囚人たちは作戦会議では、各色への 0, 1 の数の割り当てと、それぞれが偶数か奇数かの担当を決めておけばよい
ということになります。
もっというと、このパズル1では、 a0 は帽子色の合計が 2 で割って余り 0 になる場合を担当し、a1 は帽子色の合計が 2 で割って余り 1 になる場合を担当しています。

これで、数学を使った理解でパズル1を説明することができました。
それでは、5人5色のパズル中級編の解説に進みましょう。
囚人と帽子のパズル(中級編)の解説
それでは、パズル2(中級編)の囚人側の必勝戦略について解説していきます。
まず、囚人たちは作戦会議にて
- 5 色の色に 0 から 4 の数字を割り当てます
- そして自分たち囚人にも a0 から a4 という役割を 1 つずつ割り当てます。
そして、その戦略とは、
「見えた色の合計と自分の発言した色の合計を 5 で割った結果が、余り =自分の囚人番号と になるように発言する」
というものです
例えば囚人 a0 の役割は、
「見えた色の合計と自分の発言した色の合計を 5 で割った結果が余り 0 になるように発言する」
ことになります。
ここからは、図と表を用いて解説していきます。
看守によって以下のように帽子を被せられたとします。
まず、その時の囚人と帽子の色を表にします。
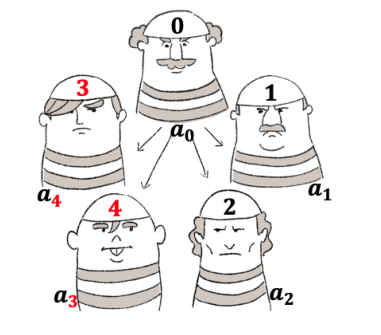

次に、各囚人が計算した、自分以外の見えた帽子の色の合計を追加します。

例えば a0 の「見えた色の合計」に 10 が書いてあるのは、a0 以外の帽子の数字(の色がついてる部分)を全て足したからです。
さらに、
- 各囚人が役割に沿って、どのように発言したか
- そして正解したかどうか
を書き込んでいきます。それが以下のようになります。

この表を見ていただき、
「見えた色の合計と自分の発言した色の合計を 5 で割った結果が、余り =自分の囚人番号と になるように発言する」
とどうなるか考えていきましょう。
例えば a0 に着目してみます。 a0 はなぜ0 と発言したかというと、
- 見えた色の合計が 10
- 発言できるのは、 0 から 4 の数のどれかで、見えた色の合計(10)と足して 5 で割った時に余りが 0 になるのは 0 だけ
なので 0 と発言しました。
またこの時の全囚人の帽子の色の合計は、5 で割って 0 余る数である 10 になっており、そのことからも a0 が正解できたのが分かります。
他の囚人が正解したかどうかを見ると a0 以外の囚人は不正解でしたが、
1 人は正解したので囚人側の勝利です。
このように、この戦略を用いれば、必ず 1 人は正解していることが確認できました。
(気になる方は、紙とペンを用意して、好きに帽子を被せてみて、同じように各囚人たちの発言をメモしていってみてください。必ず 1 人は正解していることが確認できるはずです。
そして先に全囚人の帽子の色の合計を計算しておけば、どの囚人が正解するか
を予想をつけることもできます。)
いかがでしたでしょうか?
今回はパズル 1 の人数と帽子の色の数を同時に、2 つから 5 つへ変えて別のパズル(パズル 2)を作りました。そしてどちらのパズルも同様に常に 1 人以上が正解する戦略が存在することが分りました。
なので囚人たちの勝利条件が、正解者が 1 人以上ということならば、どちらのゲームにも囚人側に必勝戦略が存在することになります。
ところで、このパズル2では、囚人と色の数は 5 つとは言わず 10 でも 100 でも 1 億でも同じことができます。
(もちろん例えば色の数が 1億 ならば、全員が一度も足し算を間違うことがないのか?なんて気になってしまいますが、囚人たちはそんなミスをしないということにしておきましょう。)
なので、パズル 1やパズル2のようなゲーム、つまり、
囚人と色の数が同じならば、どんな数になっても囚人側は必勝戦略を持つという一般的な定理が得られます。
数学的に言い換えるならば、
定理.
n を 2 以上の自然数とする。囚人の人数も色の数もどちらも n であること以外はパズル 1 と同じであるゲームにおいて、囚人たちには必勝戦略が存在する。
となります。
・・・それでは、囚人の人数や色の数が無限になると、いったいどうなるのでしょうか?
それこそが、まさに私の研究である、帽子パズルの無限化というテーマです。
数学の分野では、(公理的)集合論という無限を研究対象とした数学があり、集合論の知識を活かしながら、帽子パズルの無限化というテーマに取り組んでいます。
後編では、無限にするとどんな定理が成り立つのか、集合論の知識を活かしながら、考察していきたいと思います。
集合論は、数学 A などで学ぶ集合と同じところから出発するので、気軽に読み進めてもらえばと思います!
帽子パズルTips
ちなみに、帽子パズルには、以下の点が共通している様々なバリエーションが存在します。最後にこれらを少し紹介したいと思います。
様々なバリエーションの帽子パズルの共通点
- どの囚人も色付きの(もしくは互いに区別のつくどの囚人から見ても判別できる何か、例えば数字とか)帽子を被せられる
- どの囚人も自身の帽子の色はわからない
- どの囚人も自身の色について推測する、または色のいずれか 1 つを発言する
様々なバージョンの例
- 一定の正解数を要求されるというルールが変わったもの
- ルールはこれまで同様なものの、囚人数・色の数の組み合わせが変わったもの(例えば囚人は 2 人、色の数は 5 色なんてのもアリ)
- 各囚人の帽子の見え方が変わったもの
- 色の発言が同時でないもの
例えば、
③のパターンでは、ある囚人が立ち位置を変えるなどして見えない帽子があるようにしたり、④のパターンでは、例えばある囚人が発言した後にそれを聞いた残りの囚人が同時に発言するなどがあり、他には、パズル2のような状況でa0, a1, a2, a3, a4 の順番に1人ずつ発言していく(もちろん自分より前の発言はすべて聞くことができる)などのパターンも存在します。
これらのパズルを解説しているおすすめ動画を紹介しておきます。どちらもナレーションは英語ですが、丁寧に作られたアニメーションで、理解しやすいので、ぜひ見てみてくださいね!
『Can you solve the prisoner hat riddle? – Alex Gendler』(囚人の帽子のなぞなぞを解けるか?)
『Prisoner Hat PUZZLE ——10 Prisoners —— RED & BLUE Hats』(囚人の帽子のパズル —— 10人の囚人 —— 赤と青の帽子)
本記事は数学専攻博士課程院生の静間 荘司(@souji04261)さんによる寄稿記事です。
寄稿いただいた静間さんは帽子パズル研究をさらに推進・宣伝すべく、2023年1月よりacademistという研究者向けクラウドファンディングサービスにて月額支援型プロジェクト「「囚人と帽子のパズル」の無限化を通して、新たな数学の公理を作る」に挑戦中です。
帽子パズル研究の最先端の情報や、静間さんの数学に関する活動(大人向けの数学の個人レッスンや勉強会)について興味のある方は是非ご覧ください!